TALES DE MILETO: "Los 5 Teoremas".

Son cinco sus teoremas geométricos:

Teorema1. Todo ángulo inscrito en una semicircunferencia es recto 

                                                          

Como OA y OB son iguales, Los ángulos ABO y BOA también son iguales y como OA y OC son iguales, los ángulos OAC y OCA son iguales. Por tanto, BAC es la suma de ABC y ACB, teniendo en cuenta que la suma de los tres ángulos de un triángulo BAC debe ser recto.

Teorema 2. Todo diámetro bisecta a la circunferencia

Es un teorema de geometría particularmente enfocado a los triángulos rectángulos, las circunferencias y los ángulos inscritos, consiste en el siguiente enunciado:
Sea B un punto de la circunferencia de diámetro AC, distinto de A y de C. Entonces el ángulo ABC, es recto.
Este teorema es un caso particular de una propiedad de los puntos cocíclicos y de la aplicación de los ángulos inscritos dentro de una circunferencia.

                                   

Teorema 3. Los ángulos en la base de un triángulo isósceles son iguales.

Parte de la leyenda atribuye a Tales el uso de sus conocimientos de geometría para medir las dimensiones de las pirámides de Egipto y calcular la distancia a la costa de barcos en alta mar. Diógenes Laertes, junto con Plinio y Plutarco señalan que la medida de la altura de las pirámides se llevó a cabo a través de la determinación de la longitud de la sombra que ellas producían cuando una vara clavada verticalmente en el suelo producía una sombra igual a su altura. Para medir la distancia de los barcos en alta mar a la costa, la leyenda dice que Tales fue el primero en emplear la proporcionalidad de los lados de triángulos semejantes. Hay dudas muy grandes con respecto a esto, ya que estas ideas se habían manejado con mucha anterioridad en Egipto y Mesopotamia, donde Tales invirtió una parte de su vida. Queda entonces planteada la interrogante de si Tales fue el primer hombre en la historia en introducir estructuras lógicas en la geometría. Es muy posible que el verdadero papel que haya jugado no sea tanto el de creador y esté más relacionado con el de un intérprete, organizador y recopilador inteligente de esas estructuras lógicas.

Teorema 4. Los ángulos opuestos por el vértice son iguales

Teorema 5. Dos triángulos que tienen dos ángulos y un lado respectivamente iguales son iguales.

Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes. Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de los lados del triángulo, se obtiene otro triángulo AB'C', cuyos lados son proporcionales a los del triángulo ABC. Lo que se traduce en la fórmula.                                                         
                                                                   
                                                                 

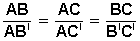
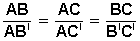
Sobre el conocido Teorema de Tales, tal vez no fuera Tales su autor, sin embargo, se le ha atribuido a él por utilizarlo para medir distancias.